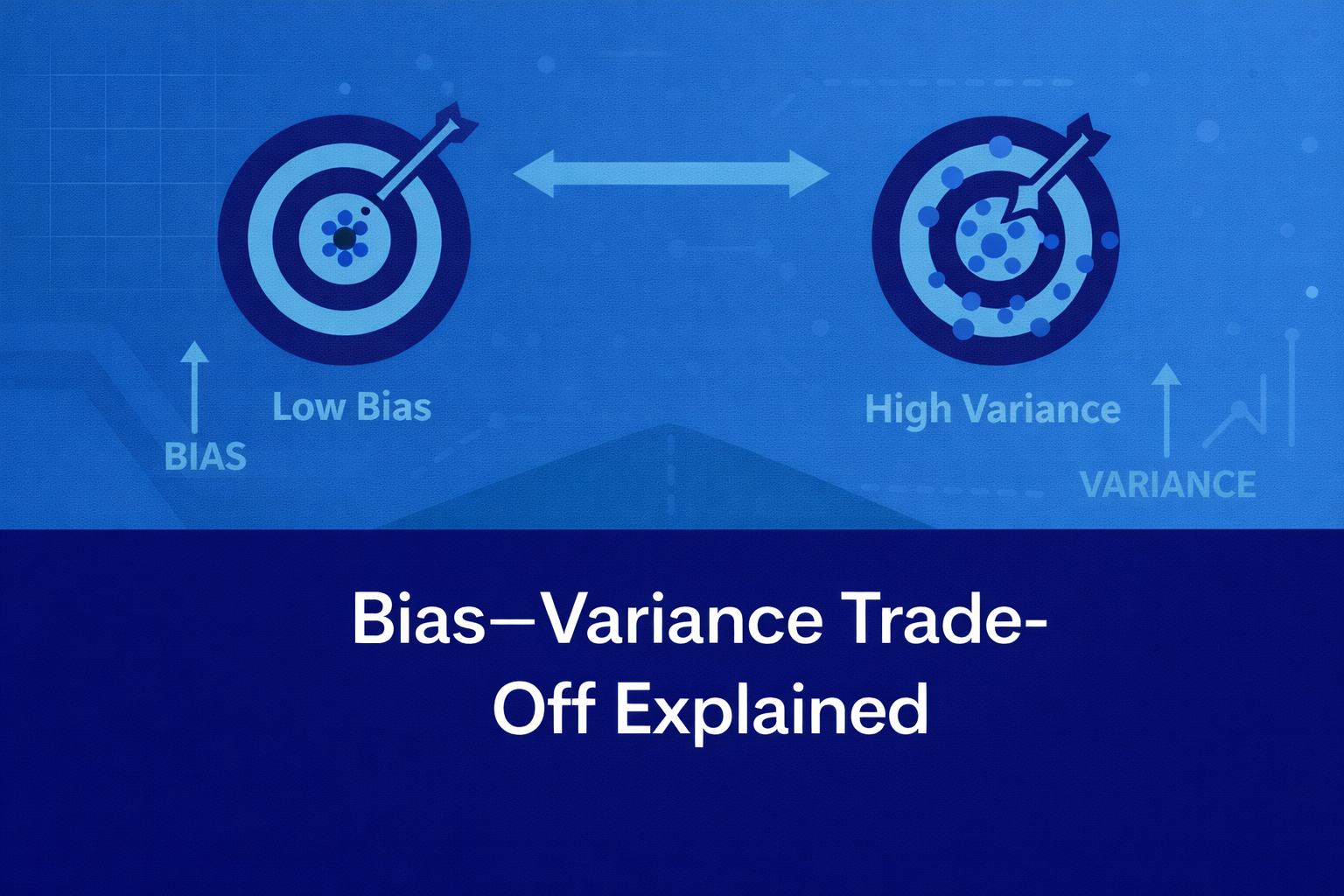
The bias–variance trade-off is not just a theoretical concept—it is the core tension that governs model generalization.
When interviewers ask about it, they are evaluating whether you understand:
- Why models overfit
- Why models underfit
- How complexity impacts performance
- How to design systems that generalize beyond training data
At its heart, the bias–variance trade-off explains why increasing model complexity does not always improve real-world performance.
The Big Idea: Prediction Error Has Three Components
In supervised learning, total prediction error can be decomposed into:Total Error=Bias2+Variance+Irreducible Error
Let’s break this down.
1. Bias
Error caused by wrong assumptions in the model.
2. Variance
Error caused by sensitivity to small changes in training data.
3. Irreducible Error
Noise inherent in the data (cannot be eliminated).
The trade-off exists because reducing bias often increases variance, and reducing variance often increases bias.
Understanding Bias: Systematic Error
What Is Bias?
Bias measures how far the model’s average prediction is from the true underlying relationship.
High bias means:
- Model is too simple
- It fails to capture real patterns
- It underfits
Example
Imagine trying to model a curved relationship using linear regression.
The straight line cannot capture curvature.
That systematic error is bias.
Characteristics of High Bias
- Poor performance on training data
- Poor performance on validation data
- Oversimplified assumptions
Interview Signal
When candidates say:
“A high-bias model is underfitting the data.”
That’s correct—but senior candidates go further:
“The model’s hypothesis space is too constrained to represent the underlying distribution.”
That’s depth.
Understanding Variance: Sensitivity to Data
What Is Variance?
Variance measures how much the model’s predictions fluctuate when trained on different subsets of data.
High variance means:
- Model is too complex
- It memorizes training data
- It overfits
Example
A deep neural network trained on a small dataset:
- Perfect training accuracy
- Poor validation accuracy
The model is capturing noise.
Characteristics of High Variance
- Excellent training performance
- Poor validation/test performance
- Sensitive to minor data changes
Interview Signal
Strong candidates mention:
“High variance models have low bias but fail to generalize.”
The Trade-Off: Why It Exists
As model complexity increases:
- Bias ↓ (model becomes more flexible)
- Variance ↑ (model becomes more sensitive)
As model complexity decreases:
- Bias ↑ (model too rigid)
- Variance ↓ (model more stable)
There is an optimal complexity level where validation error is minimized.
This is the sweet spot of generalization.
Visualizing the Trade-Off (Conceptually)
Imagine model complexity on the x-axis and error on the y-axis:
- Training error always decreases as complexity increases.
- Validation error decreases first (bias reduces), then increases (variance dominates).
Interviewers love when candidates describe this curve verbally—it shows intuition.
Real-World Implications in Model Design
Low Complexity Models
Examples:
- Linear regression
- Shallow decision trees
Pros:
- Stable
- Interpretable
- Low variance
Cons:
- May underfit complex relationships
High Complexity Models
Examples:
- Deep neural networks
- Large ensembles
Pros:
- Capture complex patterns
- Low bias
Cons:
- Overfitting risk
- Higher compute cost
- Harder to interpret
Production ML is about managing this tension.
Diagnosing Bias vs Variance in Practice
Interviewers often ask:
“How would you detect if your model suffers from high bias or high variance?”
High Bias Indicators
- High training error
- High validation error
- Both errors similar
High Variance Indicators
- Low training error
- High validation error
- Large gap between train and validation
Recognizing these patterns quickly is a strong interview signal.
Techniques to Reduce Bias
If bias is high (underfitting):
- Increase model complexity
- Add features
- Reduce regularization
- Use nonlinear models
Techniques to Reduce Variance
If variance is high (overfitting):
- Increase training data
- Apply regularization (L1/L2)
- Use dropout (deep learning)
- Prune decision trees
- Use cross-validation
- Simplify model
Senior candidates mention regularization before switching models.
How Interviewers Evaluate This Topic
They are looking for:
- Conceptual clarity
- Ability to connect bias/variance to overfitting/underfitting
- Understanding of training vs validation behavior
- Practical mitigation strategies
- Awareness of model complexity trade-offs
Weak answer:
“Bias is underfitting, variance is overfitting.”
Strong answer:
“Bias reflects model assumptions limiting representation capacity, while variance reflects sensitivity to training data fluctuations. Model complexity mediates this trade-off.”
That’s the difference between textbook and practitioner.
Beyond Theory: Business Impact
Bias–variance decisions affect:
- Customer experience
- Operational cost
- Safety and compliance
- Model stability over time
For example:
- High variance fraud model → too many false alerts
- High bias medical model → misses critical diagnoses
Trade-offs are not academic—they are operational.
The Hidden Interview Layer: Generalization Thinking
When interviewers ask about bias–variance, they are really testing:
“Does this candidate understand why models fail in the real world?”
Generalization is the central goal of ML.
If you understand bias–variance deeply, you understand:
- Regularization
- Cross-validation
- Ensemble methods
- Early stopping
- Model selection strategy
It’s the conceptual backbone of ML.
Final Thought: Balance Is the Goal
The bias–variance trade-off teaches one fundamental lesson:
A perfect training model is often a bad production model.
Strong ML engineers do not chase lowest training error.
They optimize for robust generalization.
If you can articulate:
- What bias is
- What variance is
- Why they oppose each other
- How to diagnose and fix each
- How complexity influences both
You demonstrate mastery—not memorization.